时间序列预测算法-DSP
2 分钟阅读
时间序列预测是指使用过去的时间序列数据来预测未来的值。时间序列数据通常包括时间和相应的数值,例如资源用量、股票价格或气温。时间序列预测算法 DSP(Digital Signal Processing)是一种数字信号处理技术,可以用于分析和处理时间序列数据。
离散傅里叶变换(DFT)就是DSP领域常用的一种算法。DFT是一种将时域信号转换为频域信号的技术。通过将时域信号分解成不同的频率成分,可以更好地理解和分析信号的特征和结构。在时间序列预测中,DFT可以用于分析和预测信号的周期性和趋势性,从而提高预测的准确性。
Crane使用在数字信号处理(Digital Signal Processing)领域中常用的的离散傅里叶变换、自相关函数等手段,识别、预测周期性的时间序列。
本文将介绍DSP算法的实现流程和参数设置,以便帮助大家了解算法背后的原理,并将它应用到实际场景中。 (相关代码位于pkg/prediction/dsp目录下)
流程

预处理
填充缺失数据
监控数据在某些时间点上缺失是很常见的现象,Crane会根据前后的数据对缺失的采样点进行填充。做法如下:
假设第\(m\)个与第\(n\)个采样点之间采样数据缺失(\(m+1 < n\)),设在\(m\)和\(n\)点的采样值分别为\(v_m\)和\(v_n\),令$$\Delta = {v_n-v_m \over n-m}$$,则\(m\)和\(n\)之间的填充数据依次为$$v_m+\Delta , v_m+2\Delta , …$$
去除异常点
监控数据中偶尔会出现一些极端的异常数据点,导致这些异常点(outliers)的原因有很多,例如:
- 监控系统用0值填充缺失的采样点;
- 被监控组件由于自身的bug上报了错误的指标数据;
- 应用启动时会消耗远超正常运行时的资源
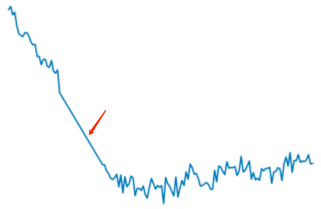
这些极端的异常点对于信号的周期判断会造成干扰,需要进行去除。做法如下:
选取实际序列中所有采样点的\(P99.9\)和\(P0.1\),分别作为上、下限阈值,如果某个采样值低于下限或者高于上限,将采样点的值设置为前一个采样值。
离散傅里叶变换
对监控的时间序列(设长度为\(N\))做快速离散傅里叶变换(FFT),得到信号的频谱图(spectrogram),频谱图直观地表现为在各个离散点\(k\)处的「冲击」。 冲击的高度为\(k\)对应周期分量的「幅度」,\(k\)的取值范围\((0,1,2, … N-1)\)。
\(k = 0\)对应信号的「直流分量」,对于周期没有影响,因此忽略。
由于离散傅里叶变换后的频谱序列前一半和后一半是共轭对称的,反映到频谱图上就是关于轴对称,因此只看前一半\(N/2\)即可。
\(k\)所对应的周期$$T = {N \over k} \bullet SampleInterval$$
要观察一个信号是不是以\(T\)为周期,至少需要观察两倍的\(T\)的长度,因此通过长度为\(N\)的序列能够识别出的最长周期为\(N/2\)。所以可以忽略\(k = 1\)。
至此,\(k\)的取值范围为\((2, 3, … , N/2)\),对应的周期为\(N/2, N/3, …\),这也就是FFT能够提供的周期信息的「分辨率」。如果一个信号的周期没有落到\(N/k\)上,它会散布到整个频域,导致「频率泄漏」。 好在在实际生产环境中,我们通常遇到的应用(尤其是在线业务),如果有规律,都是以「天」为周期的,某些业务可能会有所谓的「周末」效应,即周末和工作日不太一样,如果扩大到「周」的粒度去观察,它们同样具有良好的周期性。
Crane没有尝试发现任意长度的周期,而是指定几个固定的周期长度(\(1d、7d\))去判断。并通过截取、填充的方式,保证序列的长度\(N\)为待检测周期\(T\)的整倍数,例如:$$T=1d,N=3d;T=7d,N=14d$$。
我们从生产环境中抓取了一些应用的监控指标,保存为csv格式,放到pkg/prediction/dsp/test_data目录下。
例如,input0.csv文件包括了一个应用连续8天的CPU监控数据,对应的时间序列如下图:
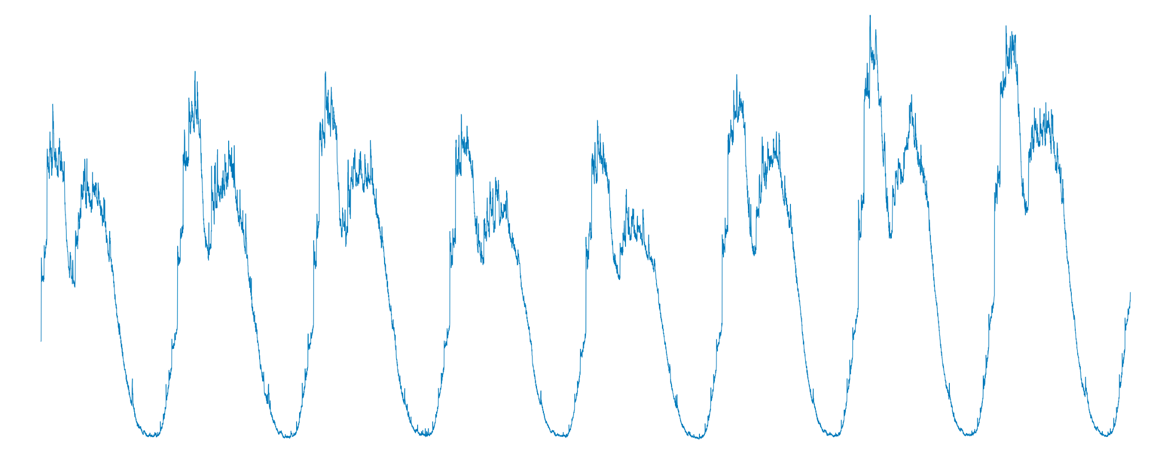
我们看到,尽管每天的数据不尽相同,但大体「模式」还是基本一致的。
对它做FFT,会得到下面的频谱图:
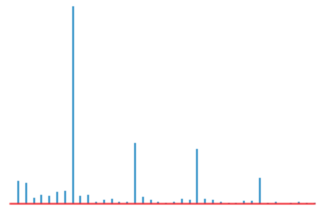
我们发现在几个点上的「幅值」明显高于其它点,这些点便可以作为我们的「候选周期」,待进一步的验证。
上面是我们通过直觉判断的,Crane是如何挑选「候选周期」的呢?
对原始序列\(\vec x(n)\)进行一个随机排列后得到序列\(\vec x’(n)\),再对\(\vec x’(n)\)做FFT得到\(\vec X’(k)\),令\(P_{max} = argmax|\vec X’(k)|\)。
重复100次上述操作,得到100个\(P_{max}\),取\(P99\)作为阈值\(P_{threshold}\)。
对原始序列\(\vec x(n)\)做FFT得到\(\vec X(f)\),遍历\(k = 2, 3, …\),如果\(P_k = |X(k)| > P_{threshold}\),则将\(k\)加入候选周期。
循环自相关函数
自相关函数(Auto Correlation Function,ACF)是一个信号于其自身在不同时间点的互相关。通俗的讲,它就是两次观察之间的相似度对它们之间的时间差的函数。
Crane使用循环自相关函数(Circular ACF),先对长度为\(N\)的时间序列以\(N\)为周期做扩展,也就是在\(…, [-N, -1], [N, 2N-1], …\)区间上复制\(\vec x(n)\),得到一个新的序列\(\vec x’(n)\)。 再依次计算将\(\vec x’(n)\)依次平移\(k=1,2,3,…N/2\)后的\(\vec x’(n+k)\)与\(\vec x’(n)\)的相关系数
$$r_k={\displaystyle\sum_{i=-k}^{N-k-1} (x_i-\mu)(x_{i+k}-\mu) \over \displaystyle\sum_{i=0}^{N-1} (x_i-\mu)^2}\ \ \ \mu: mean$$
Crane没有直接使用上面的定义去计算ACF,而是根据下面的公式,通过两次\((I)FFT\),从而能够在\(O(nlogn)\)的时间内完成ACF的计算。 $$\vec r = IFFT(|FFT({\vec x - \mu \over \sigma})|^2)\ \ \ \mu: mean,\ \sigma: standard\ deviation$$
ACF的图像如下所示,横轴代表信号平移的时间长度\(k\);纵轴代表自相关系数\(r_k\),反应了平移信号与原始信号的「相似」程度。
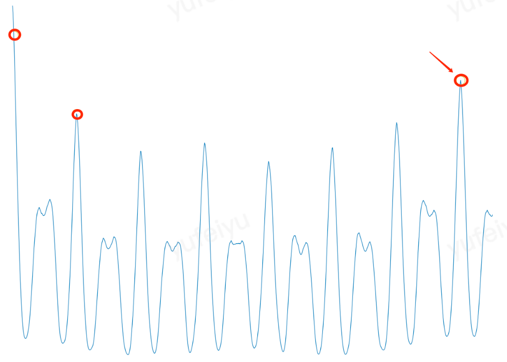
Crane会依次验证每一个候选周期对应的自相关系数是否位于「山顶」上;并且选择对应「最高峰」的那个候选周期为整个时间序列的主周期(基波周期),并以此为基础进行预测。
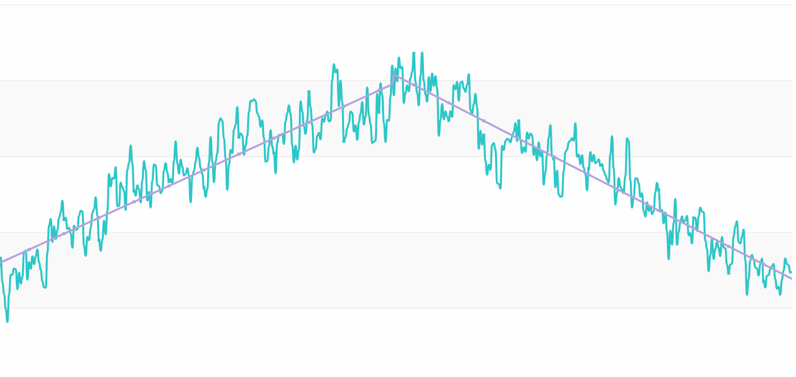
如何判断「山顶」?
Crane在两侧个各选取一段曲线,分别做线性回归,当回归后左、右的直线斜率分别大于、小于零时,则认为这个点是在一个「山顶」上。
预测
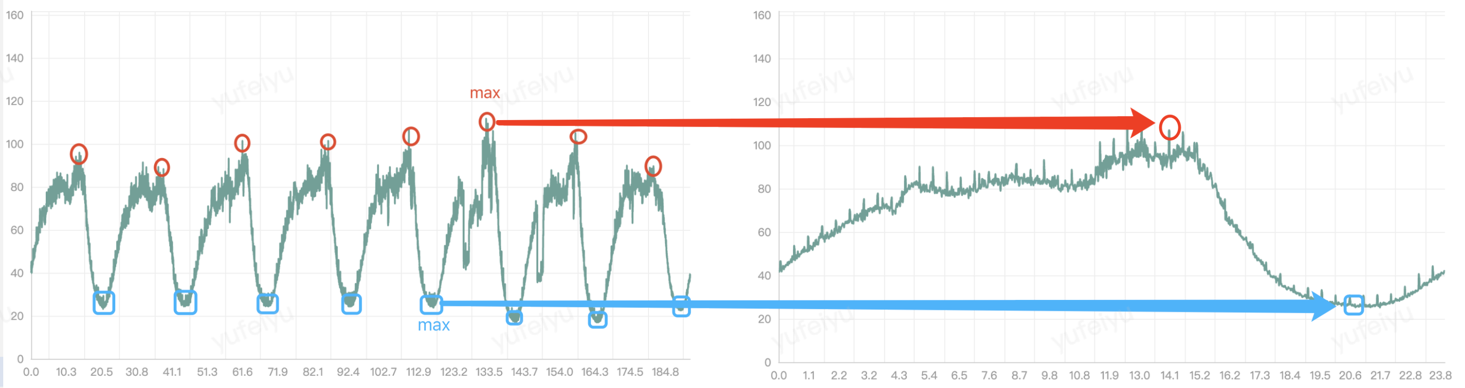
根据上一步得到的主周期,Crane提供了两种方式去拟合(预测)下一个周期的时序数据 maxValue
选取过去几个周期中相同时刻\(t\)(例如:下午6:00)中的最大值,作为下一个周期\(t\)时刻的预测值。
 fft
fft
对原始时间序列做FFT得到频谱序列,去除「高频噪声」后,再做IFFT(逆快速傅里叶变换),将得到的时间序列作为下一个周期的预测结果。
应用
Crane提供了TimeSeriesPrediction,通过这个CRD,用户可以对各种时间序列进行预测,例如工作负责的CPU利用率、应用的QPS等等。
apiVersion: prediction.crane.io/v1alpha1
kind: TimeSeriesPrediction
metadata:
name: tsp-workload-dsp
namespace: default
spec:
targetRef:
apiVersion: apps/v1
kind: Deployment
name: test
namespace: default
predictionWindowSeconds: 7200 # 提供未来7200秒(2小时)的预测数据。Crane会把预测数据写到status中。
predictionMetrics:
- resourceIdentifier: workload-cpu
type: ExpressionQuery
expressionQuery:
expression: 'sum (irate (container_cpu_usage_seconds_total{container!="",image!="",container!="POD",pod=~"^test-.*$"}[1m]))' # 获取历史监控数据的查询语句
algorithm:
algorithmType: "dsp" # 指定dsp为预测算法
dsp:
sampleInterval: "60s" # 监控数据的采样间隔为1分钟
historyLength: "15d" # 拉取过去15天的监控指标作为预测的依据
estimators: # 指定预测方式,包括'maxValue'和'fft',每一类可以指定多个estimator,配置不同的参数,crane会选取一个拟合度最高的去产生预测结果。如果不指定的话,默认使用'fft'。
# maxValue:
# - marginFraction: "0.1"
fft:
- marginFraction: "0.2"
lowAmplitudeThreshold: "1.0"
highFrequencyThreshold: "0.05"
minNumOfSpectrumItems: 10
maxNumOfSpectrumItems: 20
上面示例中的一些dsp参数含义如下:
maxValue
marginFraction: 拟合出下一个周期的序列后,将每一个预测值乘以1 + marginFraction,例如marginFraction = 0.1,就是乘以1.1。marginFraction的作用是将预测数据进行一定比例的放大(或缩小)。
fft
marginFraction: 拟合出下一个周期的序列后,将每一个预测值乘以1 + marginFraction,例如marginFraction = 0.1,就是乘以1.1。marginFraction的作用是将预测数据进行一定比例的放大(或缩小)。
lowAmplitudeThreshold: 频谱幅度下限,所有幅度低于这个下限的频率分量将被滤除。
highFrequencyThreshold: 频率上限,所有频率高于这个上限的频率分量将被滤除。单位Hz,例如如果想忽略长度小于1小时的周期分量,设置highFrequencyThreshold = 1/3600。
minNumOfSpectrumItems: 至少保留频率分量的个数。
maxNumOfSpectrumItems:至多保留频率分量的个数。
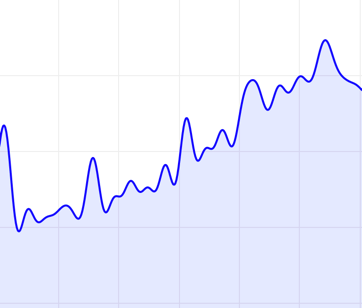
简单来说,保留频率分量的数量越少、频率上限越低、频谱幅度下限越高,预测出来的曲线越光滑,但会丢失一些细节;反之,曲线毛刺越多,保留更多细节。
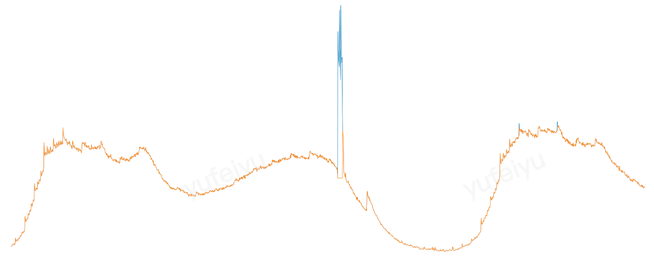
下面是对同一时段预测的两条曲线,蓝色、绿色的highFrequencyThreshold分别为\(0.01\)和\(0.001\),蓝色曲线过滤掉了更多的高频分量,因此更为平滑。
并没有一套参数配置适合所有的时间序列,通常需要根据应用指标的特点,去调整算法参数,以期获得最佳的预测效果。 Crane提供了一个web接口,使用者可以在调整参数后,直观的看到预测效果,使用步骤如下:
- 修改
TimeSeriesPrediction中的estimators的参数。 - 访问craned http server的
api/prediction/debug/<namespace>/<timeseries prediction name>,查看参数效果(如下图)。
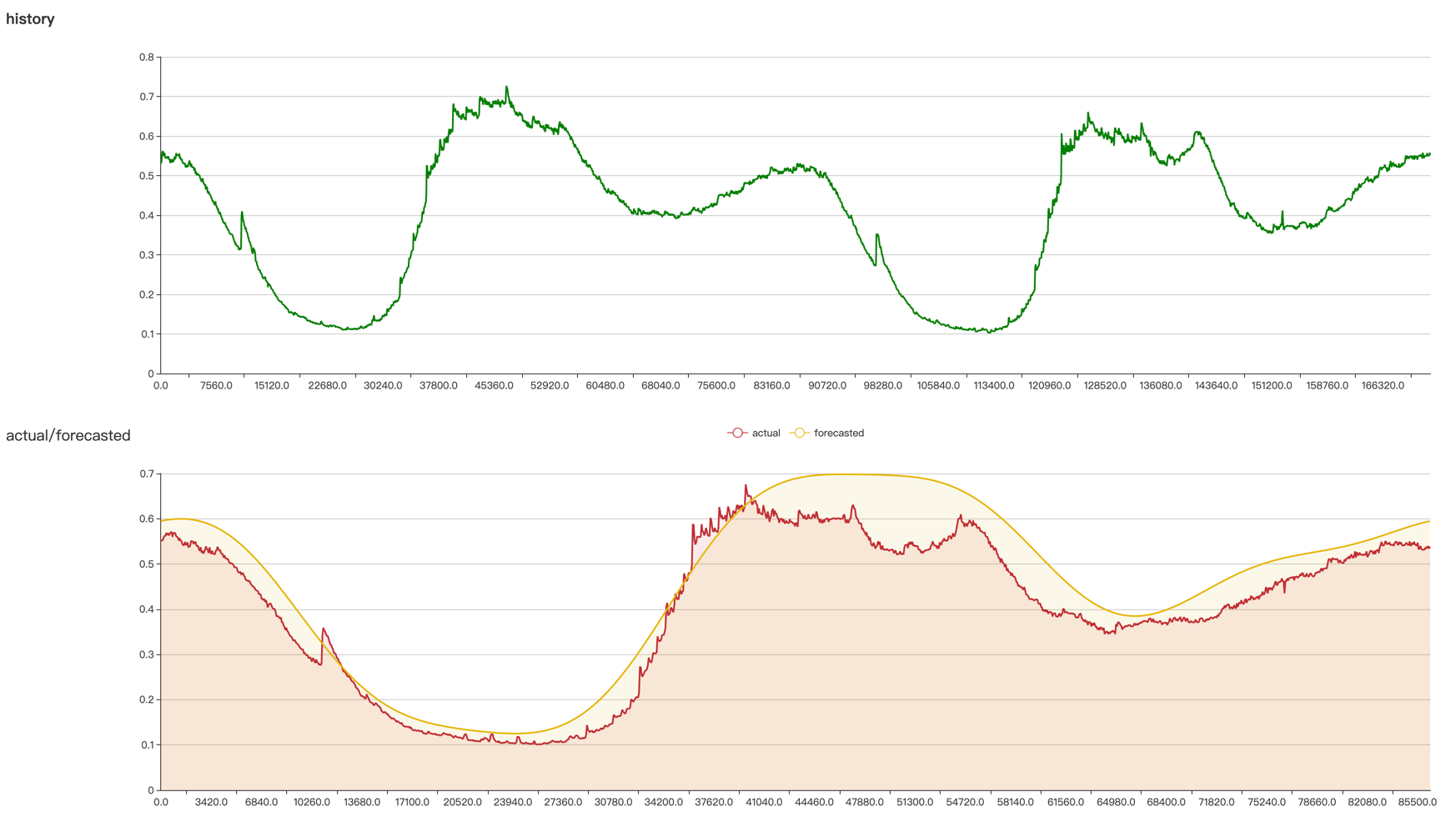
上述步骤可多次执行,直到得到满意的预测效果。
通过port-forward进行本地调试
craned http server的端口通过craned启动参数--server-bind-port设置,默认为8082。
打开终端,
$kubectl -n crane-system port-forward service/craned 8082:8082
Forwarding from 127.0.0.1:8082 -> 8082
Forwarding from [::1]:8082 -> 8082
打开浏览器,访问http://localhost:8082/api/prediction/debug/<namespace>/<timeseries prediction name>